В этой главе в основном рассмотрены методы решения задач, в которых закон движения точки выражен так называемым естественным способом: уравнением s=f(t) по заданной траектории *.

* Решения задач, в которых закон движения задан координатным способом, рассмотрены в конце главы (§ 31).

В этом случае главными параметрами, характеризующими движение точки но заданной траектории, являются: s – расстояние от заданного начального положения и t – время.

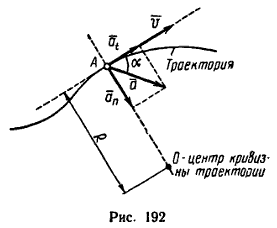
Величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью (v на рис. 192). Вектор скорости всегда направлен вдоль касательной в ту сторону, куда движется точка. Числовое значение скорости в любой момент времени выражается производной от расстояния по времени:
v = ds/dt или v = f'(t).

Ускорение a точки в каждый данный момент времени характеризует быстроту изменения скорости. При этом нужно отчетливо понимать, что скорость – вектор, и, следовательно, изменение скорости может происходить по двум признакам: по числовой величине (по модулю) и по направлению.

Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением at – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).

Числовое значение касательного ускорения в общем случае определяется по формуле
at = dv/dt или at = f''(t).

Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением an – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны (см. рис. 192).

Числовое значение нормального ускорения определяется в общем случае по формуле
an = v2/R,
где v – модуль скорости точки в данный момент;
R – радиус кривизны траектории в месте, где находится точка в данный момент.

После того как определены касательное и нормальное ускорения, легко определить и ускорение a (полное ускорение точки).

Так как касательная и нормаль взаимно перпендикулярны, то числовое значение ускорения а можно определить при помощи теоремы Пифагора:
a = sqrt(at2 + an2).

Направление вектора a можно определить, исходя из тригонометрических соотношений, по одной из следующих формул:
sin = an/a; cos = at/a; tg = an/at.

Но можно сначала определить направление полного ускорения a использовав формулу tg = an/at,
а затем найти числовое значение a:
a = an/sin или a = at/cos .

Касательное и нормальное ускорения точки являются главными кинематическими величинами, определяющими вид и особенности движения точки.

Наличие касательного ускорения (at0) или его отсутствие (at=0) определяют соответственно неравномерность или равномерность движения точки.

Наличие нормального ускорения (an0) или его отсутствие (an=0) определяют криволинейность или прямолинейность движения точки.

Движение точки можно классифицировать так:
а) равномерное прямолинейное (at = 0 и an = 0);
б) равномерное криволинейное (at = 0 и an 0);
в) неравномерное прямолинейное (at 0 и an = 0);
г) неравномерное криволинейное (at 0 и an 0).

Таким образом, движение точки классифицируется по двум признакам: по степени неравномерности движения и по виду траектории.

Степень неравномерности движения точки задана уравнением s=f(t), а вид траектории задается непосредственно.

§ 27. Равномерное прямолинейное движение точки

Если at=0 и an=0, то вектор скорости остается постоянным (v=const), т. е. не изменяется ни по модулю, ни по направлению. Такое движение называется равномерным прямолинейным.

Уравнение равномерного движения имеет вид
(а) s = s0 + vt
или в частном случае, когда начальное расстояние s0=0,
(б) s = vt.

В уравнение (а) входит всего четыре величины, из них две переменные: s и t и две постоянные: s0 и v. Поэтому в условии задачи на равномерное и прямолинейное движение точки должны быть заданы три любые величины.

При решении задач необходимо выяснить все заданные величины и привести их к одной системе единиц. При этом нужно заметить, что как в системе МКГСС (технической), так и в СИ единицы всех кинематических величин одинаковы: расстояние s измеряется в м, время t – в сек, скорость v – в м/сек.

§ 28. Равномерное криволинейное движение точки

Если at = 0 и an 0, то модуль скорости остается неизменным (точка движется равномерно), но ее направление изменяется и точка движется криволинейно. Иначе, при равномерном движении по криволинейной траектории точка имеет нормальное ускорение, направленное по нормали к траектории и численно равное
an = v2/R,
где R – радиус кривизны траектории.

В частном случае движения точки по окружности (или по дуге окружности) радиус кривизны траектории во всех ее точках постоянный:
R = r = const,
а так как и числовое значение скорости постоянно, то
an = v2/r = const.

При равномерном движении числовое значение скорости определяется из формулы
v = (s - s0)/t или v = s/t.

Если точка совершит полный пробег по окружности, то путь s равен длине окружности, т. е. s = 2r = d (d = 2r – диаметр), а время равно периоду, т. е. t = T. Выражение скорости примет вид
v = 2r/T = d/T.

§ 29. Равнопеременное движение точки

Если вектор at=const (касательное ускорение постоянно как по модулю, так и по направлению), то an=0. Такое движение называется равнопеременным и прямолинейным.

Если же постоянным остается только числовое значение касательного уравнения
at = dv/dt = f'(t) = const,
то an0 и такое движение точки называется равнопеременным криволинейным.

При |at|>0 движение точки называется равноускоренным, а при |at|<0 – равнозамедленным.

Уравнение равнопеременного движения независимо от его траектории имеет вид
(1) s = s0 + v0t + att2 / 2.

Здесь s0 – расстояние точки от исходного положения в момент начала отсчета; v0 – начальная скорость и at – касательное ускорение – величины численно постоянные, a s и t – переменные.

Числовое значение скорости точки в любой момент времени определяется из уравнения
(2) v = v0 + att.

Уравнения (1) и (2) являются основными формулами равнопеременного движения и они содержат шесть различных величин: три постоянные: s0, v0, at и три переменные: s, v, t.

Следовательно, для решения задачи на равнопеременное движение точки в ее условии должно быть дано не менее четырех величин (систему двух уравнений можно решить лишь в том случае, если они содержат два неизвестных).

Если неизвестные входят в оба основных уравнения, например, неизвестны at и t, то для удобства решения таких задач выведены вспомогательные формулы:

после исключения at из (1) и (2)
(3) s = s0 + (v + v0)t / 2;

после исключения t из (1) и (2)
(4) s = s0 + (v2 - v02) / (2at).

В частном случае, когда начальные величины s0=0 и v0=0 (равноускоренное движение из состояния покоя), то получаем те же формулы в упрощенном виде:
(5) s = att2 / 2;
(6) v = att;
(7) s = vt / 2;
(8) s = v2 / (2at).

Уравнения (5) и (6) являются основными, а уравнения (7) и (8) – вспомогательными.

Равноускоренное движение из состояния покоя, происходящее под действием только силы тяжести, называется свободным падением. К этому движению применимы формулы (5)–(8), причем
at = g = 9,81 м/сек2 9,8 м/сек2.

§ 30. Неравномерное движение точки по любой траектории

Задача 155. Движение точки по прямолинейной траектории описывается уравнением s = 0,2t3 - t2 + 0,6t (s – в м, t – в сек)...

§ 31. Определение траектории, скорости и ускорения точки, если закон ее движения задан в координатной форме

Если точка движется относительно некоторой системы координат, то координаты точки изменяются с течением времени. Уравнения, выражающие функциональные зависимости координат движущейся точки от времени, называют уравнениями движения точки в системе координат (см. § 51, п. 2 в учебнике Е. М. Никитина).

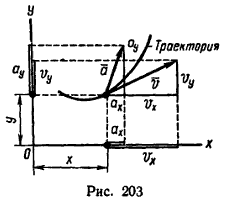
Движение точки в пространстве задается тремя уравнениями:
x = f1(t);
(1) y = f2(t);
z = f3(t);

Движение точки в плоскости (рис. 203) задается двумя уравнениями:
(2) x = f1(t);
y = f2(t);

Системы уравнений (1) или (2) называют законом движения точки в координатной форме.

Ниже рассматривается движение точки в плоскости, поэтому используется только система (2).

Если закон движения точки задан в координатной форме, то:

а) траектория плоского движения точки выражается уравнением
y = F(x),
которое образуется из данных уравнений движения после исключения времени t;

б) числовое значение скорости точки находится из формулы
v = sqrt(vx2 + vy2)
после предварительного определения проекции (см. рис. 203) скорости на оси координат
vx = dx/dt и vy = dy/dt;

в) числовое значение ускорения находится из формулы
a = sqrt(ax2 + ay2)
после предварительного определения проекций ускорения на оси координат
ax = dvx/dt и ay = dvy/dt;

г) направления скорости и ускорения относительно осей координат определяются из тригонометрических соотношений между векторами скорости или ускорения и их проекциями.

Задача 157. Движение точки A задано уравнениями: x = 2t2 + 2; y = 1,5t2 + 1, где x и y – в см, а t – в сек. Определить...

§ 32. Кинематический способ определения радиуса кривизны траектории

При решении многих технических задач возникает необходимость знать радиус кривизны R (или 1/R – кривизну) траектории. Если задано уравнение траектории, то радиус ее кривизны в любой точке можно определить при помощи дифференциального исчисления. Используя уравнения движения точки в координатной форме, можно определять радиус кривизны траектории движущейся точки без непосредственного исследования уравнения траектории. Определение радиуса кривизны траектории при помощи уравнений движения точки в координатной форме называется кинематическим способом. Этот способ основан на том, что радиус кривизны траектории движущейся точки входит в формулу
an = v2/R,
выражающую числовое значение нормального ускорения.

Отсюда
(а) R = v2/an.

Скорость v точки определяется по формуле
(б) v = sqrt(vx2 + vy2).

Следовательно,
(б') v2 = vx2 + vy2.

Числовое значение нормального ускорения an входит в выражение полного ускорения точки
a = sqrt(an2 + at2),
откуда
(в) an = sqrt(a2 - at2),
где квадрат полного ускорения
(г) a2 = ax2 + ay2
и касательное ускорение
(д) at = dv/dt.

Таким образом, если закон движения точки задан уравнениями
x = f1(t);
y = f2(t),
то при определении радиуса кривизны траектории рекомендуется произвести следующее:

1. Продифференцировав уравнения движения, найти выражения проекций на оси координат вектора скорости:
vx = f1'(t);
vy = f2'(t).

2. Подставив в (б') выражения vx и vy, найти v2.

3. Продифференцировав по t уравнение (б), полученное непосредственно из (б'), найти касательное ускорение at, а затем at2.

4. Продифференцировав вторично уравнения движения, найти выражения проекций на оси координат вектора ускорения
ax = f1''(t) = vx';
ay = f2''(t) = vy'.

5. Подставив в (г) выражения ax и ay, найти a2.

6. Подставить в (в) значения a2 и at2 и найти an.

7. Подставив в (а) найденные значения v2 и an, получить радиус кривизны R.

Задача 159. Движение точки задано уравнениями x = 3t; y = 4t - 3t2, (х, у – в см, t – в сек). Определить радиус кривизны траектории...